DETR论文
现代检测器必须要通过一大组提议、锚框或窗口中心实现回归和分类问题，他们的性能显著受到后处理步骤，为了简化这些流程，我们提出了一种直接端到端的集合预测方法，即2020年5月发表的DETR（End-to-End Detection with Transformers）。论文我将从结构剖析、创新点分析、论文收获以及根据pytorch进行代码复现。
一、模型剖析
DETR模型训练的流程简述为以下四步：
- 用CNN做特征提取为集合
- 将图片特征集合输入给transformer-encoder去学习全局的特征帮助后面做检测
- transformer-decoder生成一系列预测框集合
- 是将预测框的集合与真实框中去做匹配，在匹配上的框中再去算这个目标检测的loss去更新模型
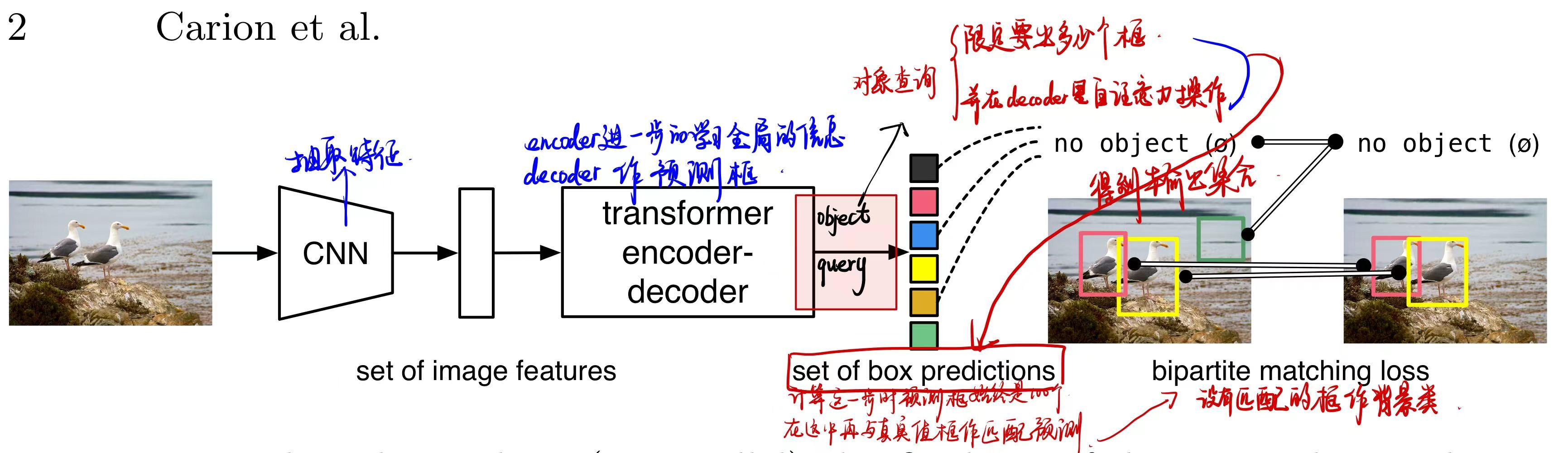
1 目标检测集合预测损失
1.1 二分匹配
设计一个基于匈牙利算法的损失函数，以找到ground-truth和预测之间的二分匹配。这强制执行了排列不变性，并保证每个目标元素都有一个唯一的匹配项。但与之前的大多数工作相比，不再使用自回归模型，而是使用具有并行解码的transformers。
基于注意力机制的transformer模型的主要优点之一是其全局计算和完美的记忆。
最低成本计算公式是：
1.2 损失计算
计算损失函数，上一步中所有匹配对的匈牙利损失
在论文中$c_i = \emptyset$时，将对数概率项的权重降低十倍，以保证类别平衡。
1.3 边界框计算
最常用的ℓ1损失对于小框和大框也会有不同的尺度。为了缓解这个问题，我们使用ℓ1损失和广义IoU损失结合：
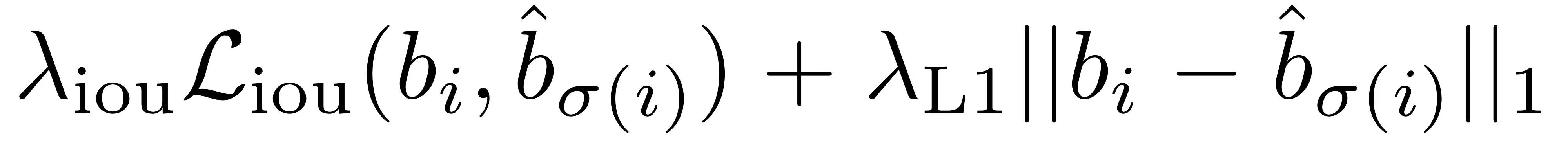
2 模型架构
一个用于提取紧凑特征表示的CNN骨干网络、一个编码器-解码器Transformer，以及一个进行最终检测预测的简单前馈网络（FFN）
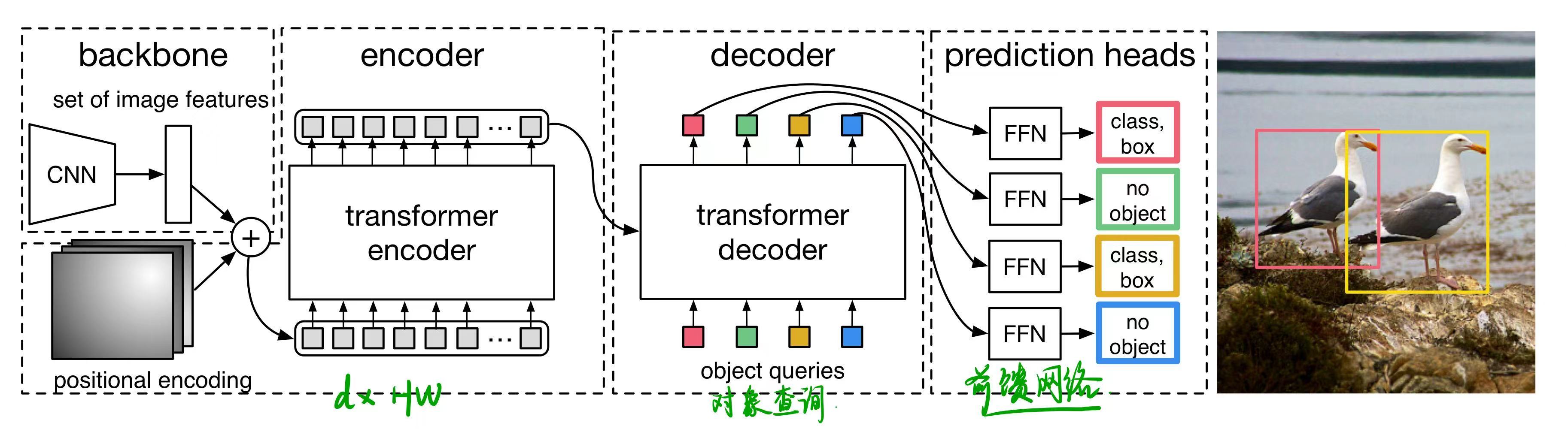
2.1 主干backbone
将输入图片$X_{img} \in \mathbb{R}^{H_{0} \times W_{0} \times C_{0}}$ 通过卷积神经网络CNN转换成$f \in \mathbb{R}^{H \times W \times C}$
注意：$C_{0}$=3；C=2048, $H = \frac{H_{0}}{32}$，$W = \frac{W_{0}}{32}$
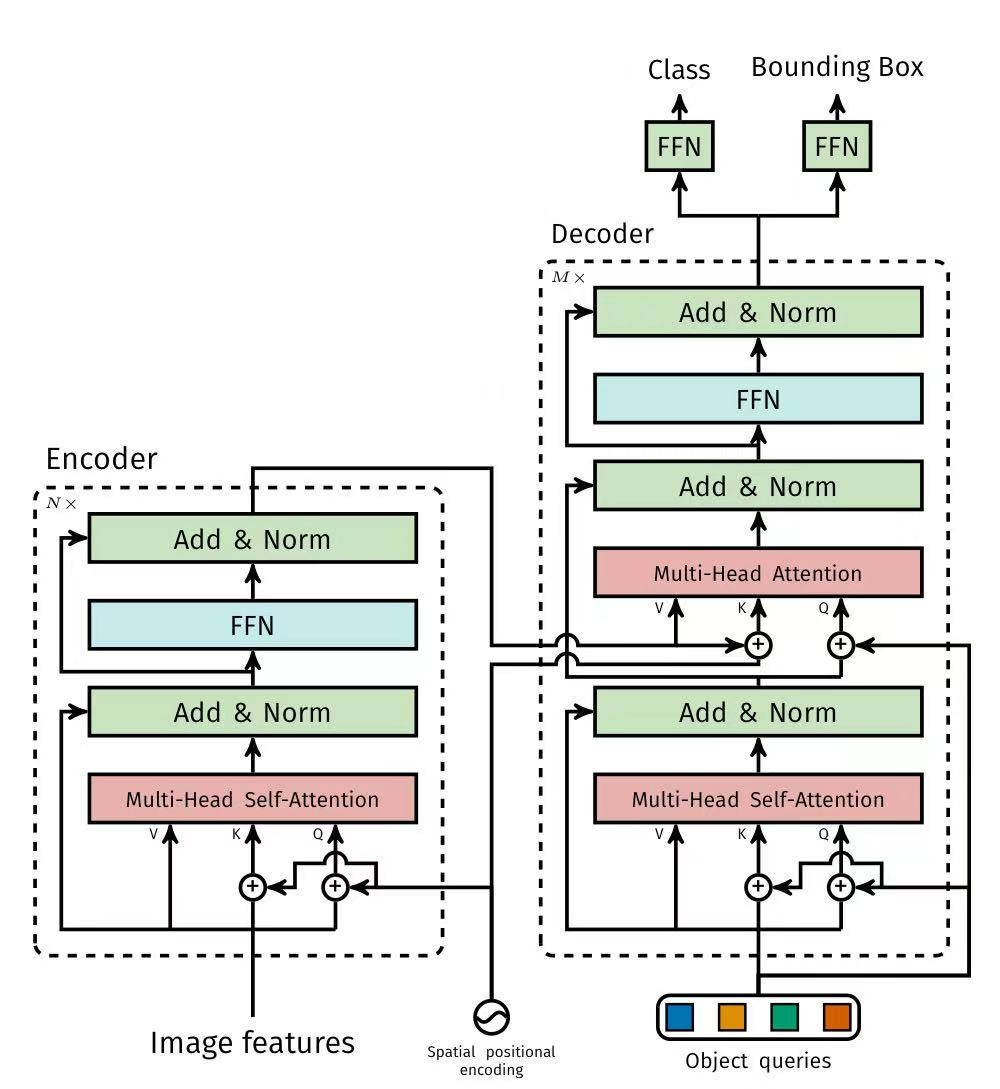
2.2 Transformer架构
2.2.1 encoder
作用：
将C降低到d（因为encoder想要的是一个序列），维度为1，序列长度则为$d \times HW$
组成：
多头注意力机制（Multi-Attention）——>信息收集与混合——>全序列交互（即综合考虑）
前馈神经网络（Feed Forward Network ）——>信息加工与提炼——>位置独立处理（即针对处理）
2.2.2 decoder
输入：解码器一开始就准备好 N个可学习的“空位”（称为“对象查询”），每个“空位”就是一个 d维的向量。
处理：解码器接收来自图像编码器的视觉特征，并通过注意力机制，让这 N个“空位”去“观察”和“理解”整张图片，并互相之间进行“沟通”（自注意力），最终把这 N个初始向量“转换”成 N个包含丰富物体信息的 d维向量（输出嵌入）。
输出：最后，每个输出嵌入（一个 d维向量）会分别通过一个简单的前馈网络，独立地预测出它对应的那个物体的类别和边界框坐标。
2.3 前馈神经网络
组成：
ReLU、隐藏维度d和线性投影层
作用：
FFN预测归一化的中心坐标、框的高度和宽度（相对于输入图像），线性层使用softmax函数预测类别标签
2.4 辅助解码损失
位置：
每个解码器层之后添加预测FFN和匈牙利损失
使用一个额外的共享层归一化来归一化来自不同解码器层的预测FFN的输入。
核心思想
“一路监督，多路受益“
辅助解码损失通过在主输出之外，额外在模型的中间层（例如解码器的某一中间层） 添加辅助的输出层，并计算损失。这个辅助损失会和主损失结合，共同指导模型参数的更新，从而让中间层也能得到更直接的训练反馈。
DETR启用辅助损失（aux_loss=True）时，模型会返回每个解码器层的输出字典列表，而不仅仅是最终层的输出。这些中间层的输出会参与到整体损失的计算中。
💡 核心作用
辅助解码损失通过其独特的工作机制，主要在以下几个方面发挥作用：
缓解梯度消失，改善训练动态：通过将损失信号“注射”到网络中间层，辅助损失提供了更短的梯度传播路径，有助于梯度更有效地反向传播，缓解深层网络中的梯度消失问题，使训练过程更稳定、收敛更快。
提供中间监督，增强表征学习：辅助损失相当于为中间层的特征学习提供了明确的监督目标，引导网络在中间层就学习到更有意义的特征表示，防止其“跑偏”，往往能使最终学到的特征更具判别力。
实现隐式模型集成：不同深度的解码层其“专业领域”可能略有不同。较低层可能捕捉更细节的局部信息，较高层则整合更全局的上下文。辅助损失鼓励这些不同层的输出都做出正确预测，其效果类似于将不同深度模型的优势进行了集成，从而可能提升最终模型的鲁棒性和泛化能力。
二、创新点
- 在detr模型中移除基于一些初始猜测进行预测这种手工设计的流程，并通过直接预测检测集合（相对于输入图像的绝对框预测，而不是锚框）来简化检测过程。两阶段检测器预测框相对于候选区域，而单阶段方法预测框相对于锚框或可能的对象中心网格。这些系统的最终性能在很大程度上取决于这些初始猜测的设置方式。
- 直接集合预测的二分匹配损失的目标检测系统的新设计。
- DETR易于实现，并且具有灵活的架构，可以轻松扩展到全景分割，并获得具有竞争力的结果。
三、论文收获
之前的似然函数和负对数似然函数学的不好，所以这次在这篇论文中重新看看
1 似然函数
1️⃣ 概念理解
似然函数：在“参数固定未知、数据已观测”的前提下，衡量“这组参数生成当前数据的合理程度”。相当于就是在调整权重参数。它和概率有很大的区别：
| 概念 | 自变量 | 含义 |
|---|---|---|
| 概率 | 数据是自变量，参数固定 | 给定参数，数据出现的可能性 |
| 似然 | 参数是自变量，数据固定 | 给定数据，参数有多合理 |
2️⃣ 数学定义
假设：
- 数据：$x_1,x_2,…,x_n$
- 模型参数：$\theta$
- 数据服从分布：$p(x \mid \theta)$
那么似然函数定义为：$\boxed{ L(\theta \mid x_1,\dots,x_n) = \prod_{i=1}^{n} p(x_i \mid \theta) }$
⚠️ 注意：
- 这是 $\theta$ 的函数
- $x_i$ 已经观测到，是常数
3️⃣ 例子（抛硬币）
- 正面概率：$\theta$
- 抛 10 次，出现 7 次正面
似然函数为：$L(\theta) = \theta^7 (1-\theta)^3$
问题变成：
哪个 $\theta$ 最可能产生“7 次正面、3 次反面”？
答案是：
$\hat{\theta} = 0.7$
这就是 最大似然估计（MLE）
2 负对数似然函数
1️⃣ 为什么要“取对数”？
似然函数是连乘：$\prod_{i} p(x_i \mid \theta)$
问题：
- 数值容易下溢（非常小）
- 计算不方便
👉 解决方案：取对数
$\log L(\theta) = \sum_{i=1}^n \log p(x_i \mid \theta)$
2️⃣ 为什么是“负”的？
在优化里：
- 我们通常 最小化损失函数
- 但 MLE 是 最大化似然
所以定义：$\boxed{ \mathcal{L}{\text{NLL}}(\theta) = - \sum{i=1}^{n} \log p(x_i \mid \theta) }$
👉 最小化负对数似然 ≡ 最大化似然函数
3 似然函数 vs 负对数似然函数（对比）
| 项目 | 似然函数 | 负对数似然 |
|---|---|---|
| 形式 | 乘积 | 求和 |
| 优化目标 | 最大化 | 最小化 |
| 数值稳定性 | 差 | 好 |
| 工程中使用 | 少 | 非常多 |
4 负对数似然 = 常见机器学习损失函数
这是重点，很多“损失函数”本质上就是 NLL 👇
1️⃣ 高斯分布 → 均方误差（MSE）
假设：$y \sim \mathcal{N}(\mu, \sigma^2$
NLL：$\mathcal{L} = \frac{1}{2\sigma^2}(y-\mu)^2 + \text{常数}$
👉 等价于最小化 MSE
2️⃣ 伯努利分布 → 交叉熵损失（Binary Cross-Entropy）
$p(y=1)=\hat y$
NLL：$-\big[y\log \hat y + (1-y)\log(1-\hat y)\big]$
👉 这就是二分类交叉熵
3️⃣ 多项分布 → Softmax + Cross Entropy
👉 深度学习分类模型的标准配置